Dimensionality reduction is a process of simplifying available data, particularly useful in statistics, and hence in machine learning.
That alone makes it very important, given that machine learning is probably the most rapidly growing area of computer science in recent times.
As evidence, let’s take this quote of Dave Waters (among hundreds of others) – “Predicting the future isn’t magic, it’s Artificial Intelligence”.
It gives machines the ability to learn on their own and carry out tasks that were only possible for humans and that too on a far smaller scale.
This itself is the engine of artificial intelligence and thus the onset of a much more efficient and convenient world.
What is Dimensionality Reduction?
Dimensionality reduction can be defined as the process of increasing the simplicity of a data set by reducing the dimension of the set (by reducing the number of random variables).
The following paragraph is a classic dimensionality reduction example.
Imagine a cube with an array of points distributed throughout. In this case, each point will need a description in three dimensions in the form of (x, y, z).
Supposing that a plane can exist which passes through most points in this cube, we can now use this plane (a square or a rectangle) for describing the points instead of the cube, in the form of (x, y).
When speaking in terms of thousands and sometimes millions of values, such reduction can mean a significant reduction in complexity.
Let us understand in a bit more detail how dimensionality reduction can help in processing large and complex datasets.
Why Dimensionality Reduction?
To understand what is dimensionality reduction, it is imperative to first understand the curse of dimensionality.
Curse of Dimensionality
Not just limited to machine learning alone, the curse of dimensionality refers to a number of phenomena that occur while organizing/analyzing data in higher dimensions. Take the following example:
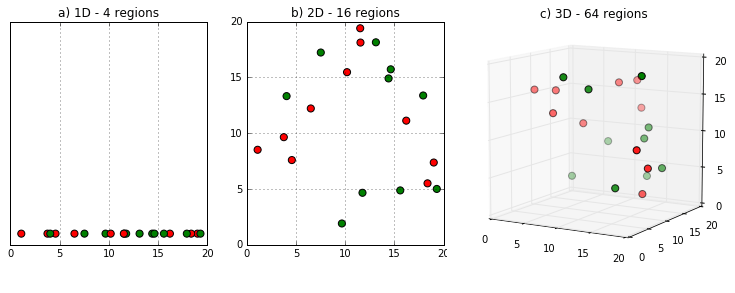
In the above example, data points lying in one dimension need only 4 spaces for describing any of the points.
In the second image, with an increase in dimension by only one (2-dimensional), the number of spaces increases to 16. And in the third image, with another addition of dimension, the number of spaces rises to 64.
This shows that as the number of dimensions increases, the amount of data needed to generalize increases exponentially.
This, in turn, affects the classifier performance. In the image that follows, it can be seen that with an increase in dimensions beyond the optimum number, classifier performance goes on decreasing.
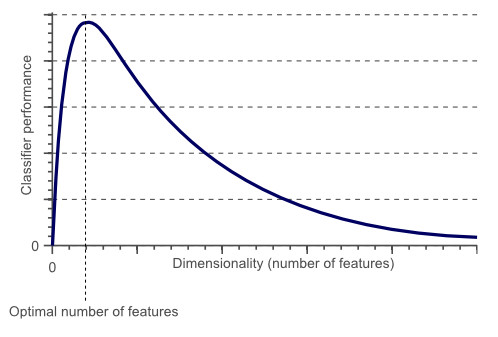
Overfitting
An important reason behind the phenomenon displayed in the above image is known as overfitting. Overfitting is when the analysis or generalization of data corresponds too exactly to a set of data.
This causes the machine to treat the noise or irregularities in the data as learning characteristics, thus affecting the accuracy of the generalized model.
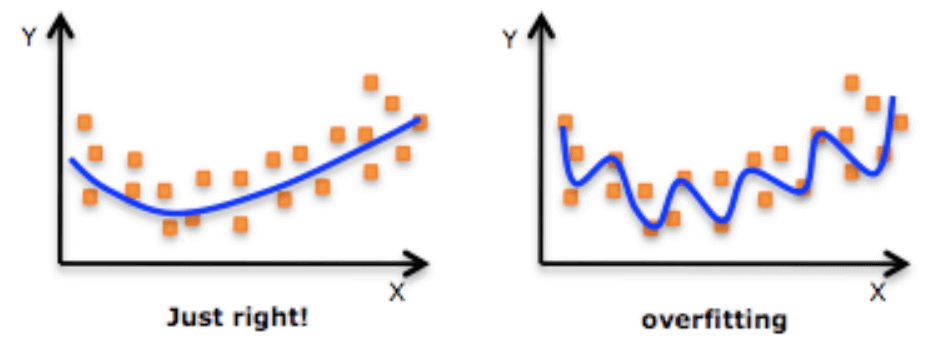
For example, a set of data about tall trees may have an incorrect entry of a tomato tree, but the model will learn it and apply it in further classification. Reducing dimensions can, in most cases, reduce the chances of overfitting.
Other Benefits
Besides the above mentioned important benefits dimensionality reduction brings, the following are some other obvious benefits that come along:
(i) Reduces the required storage space by simplifying/compressing data.
(ii) Reduces computation time by a reduction in data size.
(iii) Can help in removing redundant points.
(iv) Improves the accuracy of the model by reducing noise.
Ways to Achieve Dimensionality Reduction
The two important ways to reduce dimensions are:
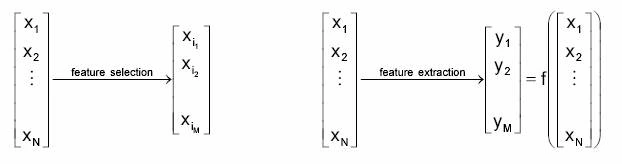
1. Feature Selection
Feature selection, as per the name, is the simple technique of selecting features that are relevant or suitable for your data processing requirements. It can be done manually by using a program. Take the following example.
Suppose we are building a model that predicts the height of a building. We have a dataset with various features including the number of windows, number of apartments, color of the building, etc.
In this dimensionality reduction example, the feature of color is hardly a deciding factor in the height of a building, and hence we can deselect this feature to simplify our dataset.
Feature selection can be divided into three types:
(i) Filters: which do not involve any learning while reducing variables.
(ii) Wrappers: which involve some learning while reducing variables.
(iii) Embedded Methods: which combine feature selection and classifier establishing
2. Feature Extraction
Unlike selection, feature extraction is the transforming of existing data into less complex data that has a reduced number of variables.
The goal here is to build derived values from the existing values, which may lead to a different but more relevant data set than the original data set.
A simple way to understand the difference between feature selection and feature extraction is this – feature selection can reduce (x, y, z) to (x, y); feature extraction can extract (2x-3y).
Besides the above-mentioned methods, feature engineering is one of the methods used, where, as the name suggests, features are engineered or created based on existing features.
It boosts the performance and accuracy of the model to a large extent but is difficult, time-consuming and often expensive.
Methods Used for Dimensionality Reduction
As mentioned previously, dimensionality reduction is all about simplifying the data set by reducing dimensions. However, this means a reduction in the total available information, which also means a decrease in the accuracy of prediction.
The goal is to use a method of dimension reduction which simplifies the data while preserving most of the information.
Going back to our dimensionality reduction example of considering a plane (square/rectangle) instead of a cube where maximum data points lie in the plane, we can see that most information can be retained while reducing the complexity of the data.
Following are two of the important methods used to achieve dimensionality reduction –
1. Principal Component Analysis
Principal component analysis (PCA) is a statistical procedure that uses an orthogonal transformation to convert a set of observations of possibly correlated variables into a set of values of linearly uncorrelated variables called principal components.
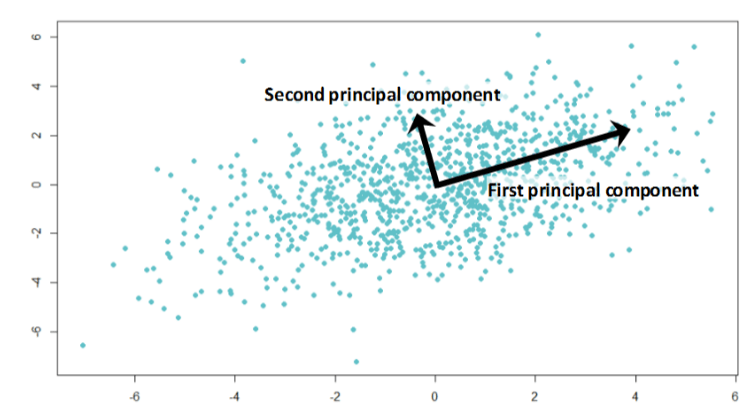
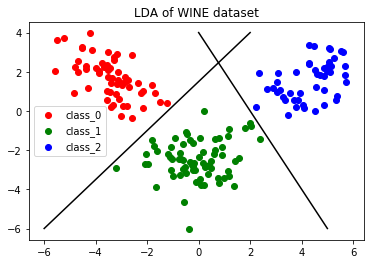
2. Linear Discriminant Analysis
Linear Discriminant Analysis works on the principle of separating variables based on classes in such a way that maximum separability is achieved.
Values from the same class are placed together while those from separate classes will be farther from each other. The image below shows a dimensionality reduction example using LDA to separate classes.
Non-linear Methods of Dimensionality Reduction
We have discussed the example of a plane passing through a cube or sphere and reducing dimensions using this plane.
But when the data points are not distributed in such simple manner such as on a single plane, linear methods cannot be used. In such a case, following non-linear methods of dimensionality reduction can be used.
(i) Multi-Dimensional Scaling
(ii) Isometric Feature Mapping
(iii) Locally Linear Embedding
(iv) Hessian Eigenmapping
(v) Spectral Embedding
(vi) T-distributed Stochastic Neighbor Embedding
Dimensionality Reduction Techniques
1. Missing Values
If there are data columns with a considerably large number of missing values, the information in the column may not turn out to be of much use.
Such columns are better removed. The more the missing values, the more is the reduction.
2. Low Variance
Data columns with negligible differences in values are not much useful too. Such low variance columns are better eliminated.
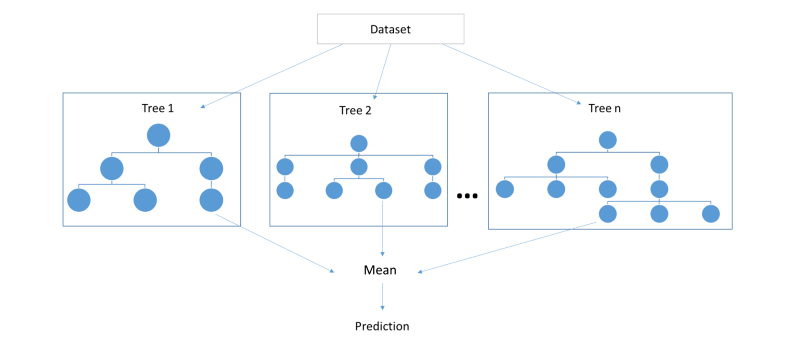
3. Random Forest
This has to do with decision trees. A large number of decision trees (mostly shallow) can be constructed with each tree trained on a small fraction of variables. This becomes a good way of feature selection.
4. Decision Trees
Similar to random forests, simply decision trees with an adequate number of branches can be used for feature selection.
5. Backward Feature Elimination
In this case, we train the model on n input features, then n-1 for the next iteration and so on for a total of n times.
The feature that causes the smallest increase in error rate is removed. This leads us with n-1, n-2 and so on a lesser number of features while not compromising on accuracy.
6. Forward Feature Construction
This is the opposite of backward feature elimination where we go on adding one feature at a time, one that produces maximum improvement inaccuracy.
Among all the dimensionality reduction techniques, forward feature construction is one of the costliest.
7. High Correlation
If two or more variables share fairly similar information, they are said to be highly correlated. In such a case, similar or almost duplicate looking data variables can be removed.
There are more techniques invented with time but the above mentioned are some of the common ones.
There is a lot more to learn about dimensionality reduction if you want to dive deeper, and the following video a Stanford lecture can help in that direction –
Disadvantages of Dimensionality Reduction
Understanding what is dimensionality reduction would be incomplete without understanding its few disadvantages.
1. Dimensionality reduction is done at the expense of loss in data, which may affect the accuracy of the model, although it simplifies it.
2. New features in PCA are not easily interpretable.
3. LDA needs labeled data.
Conclusion
The exponential rise of data science in the context of machine learning and artificial intelligence has now become an unquestionable fact.
As such, processing massive amounts of data while requiring minimum resources, viz. time, storage space and money becomes crucial.
Dimensionality reduction helps with this by reducing the complexity of a data set by significantly reducing the number of attributes required to describe variables by reducing the dimensions of the data set.
There are various statistical methods that can be employed with this goal in mind, and one should choose among the dimensionality reduction techniques by considering what suits his/her problem statement and resources best.
Data Science offers a plethora of opportunities for people who have a keen interest in science & technology. If you are also an aspiring Data Scientist, enroll in this Data Science Master Course & elevate your career.








