Data engineers are constantly involved in managing data as well as organizing the same. While doing this, they are also required to keep themselves updated regularly with the new trends and the inconsistencies which may significantly impact the business goals. Keeping this thought into consideration, we have come up with this post on bias-variance tradeoff.
According to IBM’s report “ Jobs requiring machine learning skills are paying an average of $114,000. Advertised data scientist jobs pay an average of $105,000 and advertised data engineering jobs pay an average of $117,000.”
Data engineers are highly trained technical professionals who are experts in programming, computer science, and mathematics.
Apart from this skill set, they are also required to be efficient in collecting important data trends and bias-variance tradeoff other information and then transfer it to the other teams in the organization. This would largely help in working towards the benefit of the business.
Through a supervised machine learning algorithm, the mapping function or the target function can be effectively approximated.
The machine learning algorithms prediction error can be broken down into bias and variance. Bias and variance both largely affect the machine learning algorithm.
What is Bias-Variance Tradeoff & Why is it Important?
Bias-variance tradeoff forms an essential entity of machine and statistical learning. All the learning algorithms involve a significant measure of error.
These errors can be reducible and non-reducible. We cannot do anything about non-reducible errors. The reducible errors which are the bias and variance can be made use off.
These reducible errors can be effectively minimized and the efficiency of a working system can be maximized. The main goal of a learning algorithm is to reduce these bias and variance errors to the minimum and make the most feasible model.
Achieving such a goal is not very easy that is when a tradeoff is made to reduce the possible sources of errors when a certain model is being selected based on their varied flexibility and complexity.
After understanding what is the bias-variance tradeoff, let us now focus on what is bias.
What is Bias?
Bias is used for making the learning of the target function of any model easier. This is done by making simplifying assumptions.
These simplifying assumptions are termed bias. It is basically the difference between the model’s average prediction and the actual correct value which is being attempted to be predicted by us.

When the parametric algorithms are taken into consideration, they have a high bias which makes them very easy and fast to learn and understand.
But, these are less flexible as they fail to give a high predictive performance when complex problems are being considered.
When there are fewer assumptions made about the target function form, it indicates low bias. When there are more assumptions made about the target function form, it indicates a higher bias.
What is a Variance?
If in case a different training data would be used, there would be a significant change in the estimate of the target function. Variance is the amount which indicates the variability of any model prediction in such a case.
The estimated target function here is got by the machine learning algorithm’s training data. The machine learning algorithm will have a high value of variance in its model which changes as per the training data obtained.
The specifics of this training data influence the parameters which are used for the characterization of target or mapping function.
When the changes in the training dataset suggest a small change in the estimate of the target function, there is a low variance. When the changes in the training dataset suggest a large change in the estimate of the target function, there is high variance.

Bias-Variance Tradeoff In Machine Learning For Predictive Models
The bias and variance tradeoff formula is given as follows,
Here, the first term is the irreducible error which cannot be avoided. The second and third term refers to bias and variance. The variance error can be easily eliminated by taking many samples from different models and averaging it out which is not possible in the case of bias.
This bias-variance tradeoff equation works well with both predictive as well as explanatory models. When we take the explanatory model into consideration, the main goal would be to reduce the bias to the maximum extent to get the underlying theory’s most accurate representation.
In the case of the predictive model, the main focus is not on reducing the bias to the maximum extent. A model with slightly more bias error is acceptable as long as the test set error is minimized considerably.
Here the right amount of bias and variance is found out with the main aim of test set error minimization.
This shows that the bias-variance tradeoff is more prominent and interesting in the predictive models. But, the drawback here is that the idea of achieving a true model with high accuracy is often sacrificed.
When the model is highly inflexible, we have low variance and high bias. We can easily trade the high variance for bias. Higher the flexibility of the model, lower will be the bias and higher will be the variance.
To overcome such a scenario, we will have to work towards finding the right balance of bias and variance to effectively minimize the test set error.
It is almost impossible to observe and get the true test set errors in all the cases, that is the reason bias and variance tradeoff becomes important in machine learning.
The visualization of machine learning in a bias-variance tradeoff for flexible models can be explained graphically.
The y-axis represents the test mean squared error and the x-axis represents the flexibility of the model which is under consideration.
In the graph, the squared bias is represented by the blue curve and the mean squared error is represented by the orange curve. The dashed line running through the graph represents the unavoidable or irreducible error.
Bias-Variance Tradeoff in Machine Learning for Understanding Overfitting
Overfitting is a fairly simple concept involved in machine learning which can be depicted graphically as given below.
The true shape of the data set is being depicted here in the first graphical plot. A model with zero bias has been considered which is why the line goes perfectly through all the given red dots.
Even the second plot shows almost zero bias as the shape of the blue curve is similar to the arrangement of dots.
Due to the almost zero bias, there is a high variance in the model. This is shown in the second plot. In the second plot, a model which depicts the future data set is being considered.
A large variance is shown here because the future data set being represented here deviates to a large extent from the original data set.
Through these models, it can be observed that the bias and variance tradeoff is very important for the predictive models but not for the explanatory models.
When it is for an explanatory model, the curve is fitting perfectly on the dots but when we want to predict, there a variance in the curve which means that it has been overfitted.
The X and Y relationship can be better explained in the previous plots when compared with the plots given below. Therefore, the bias-variance tradeoff is not a factor that is discussed in the explanatory models.
The plot for a model which is less flexible and for which the overfitting has not been employed can be shown graphically as follows.
There is a lot of bias observed in both the curves and the true data is not captured in both plots. The variance in the second plot is lower when compared with the first plot.
Therefore, higher predictability can be expected in the second plot due to a better choice of bias-variance tradeoff.
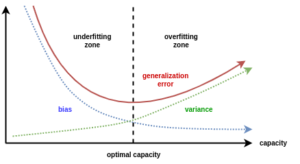
The below graph shows that with the overfitting you can expect high variance and with underfitting, you can expect high bias. Therefore, it is very important that you strike the right amount of balance between bias and variance to obtain the optimum results.
Getting The Right Bias-Variance Tradeoff

The total error has to be minimized by balancing the bias and variance for getting a good model. When you find the optimum balance of both bias and variance, it would never overfit or underfit the model which has been taken into consideration.
The optimal bias-variance tradeoff example is depicted below.
In order to get the right bias-variance tradeoff, many shrinkage methods like the lasso, ridge regression, partial least squares regression etc have been developed.
All these methods work towards shrinking or biasing the estimate coefficients so that the variance is considerably reduced.
Apart from these shrinkage methods, there are several ensemble methods like boosting, bagging, random forests, etc. These methods work to combine and average the predictions of a different variety of models to get more precise predictions.
Wrapping Up
The bias-variance tradeoff is an important concept which is used by almost every data scientist and data engineer. To employ this effectively you need to know all the basics of this concept. It proves to be very useful in machine learning for predictive as well as explanatory models.
With bias-variance tradeoff, you can effectively reduce the test set errors by finding the right balance between the bias and variance of a variety of models. It is particularly critical to understanding this concept for the prediction models.
Take up the Machine Learning using Python Course, to learn Machine Learning skills & elevate your career.
Hopefully, we have answered your question on what is a bias-variance tradeoff and provided you with relevant bias-variance examples.








