The Five Major Assumptions of Linear Regression

Before we go into the assumptions of linear regressions, let us look at what a linear regression is. Here is a simple definition.

Linear regression is a straight line that attempts to predict any relationship between two points. However, the prediction should be more on a statistical relationship and not a deterministic one. This quote should explain the concept of linear regression.

“There are many people who are together but not in love, but there are more people who are in love but not together.”

As we go deep into the assumptions of linear regression, we will understand the concept better.

What is a Linear Regression?

As explained above, linear regression is useful for finding out a linear relationship between the target and one or more predictors. In statistics, there are two types of linear regression, simple linear regression, and multiple linear regression.

Simple Linear Regression

The concept of simple linear regression should be clear to understand the assumptions of simple linear regression. In simple linear regression, you have only two variables.

One is the predictor or the independent variable, whereas the other is the dependent variable, also known as the response. A linear regression aims to find a statistical relationship between the two variables.

There is a difference between a statistical relationship and a deterministic relationship. For example, if I say that water boils at 100 degrees Centigrade, you can say that 100 degrees Centigrade is equal to 212 degrees Fahrenheit.

Thus, there is a deterministic relationship between these two variables. You have a set formula to convert Centigrade into Fahrenheit, and vice versa.

You define a statistical relationship when there is no such formula to determine the relationship between two variables. For example, there is no formula to compare the height and weight of a person. However, you can draw a linear regression attempting to connect these two variables.

An Example of Simple & Multiple Linear Regression

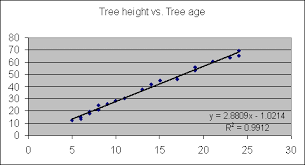
This example will help you to understand the assumptions of linear regression.

Sarah is a statistically-minded schoolteacher who loves the subject more than anything else. She assigns a small task to each of her 50 students.

There are around ten days left for the exams. She asks each student to calculate and maintain a record of the number of hours you study, sleep, play, and engage in social media every day and report to her the next morning.

All the students diligently report the information to her. At the end of the examinations, the students get their results. She now plots a graph linking each of these variables to the number of marks obtained by each student.

It is a simple linear regression when you compare two variables, such as the number of hours studied to the marks obtained by each student.

When you increase the number of variables by including the number of hours slept and engaged in social media, you have multiple variables. It explains the concept of assumptions of multiple linear regression. Naturally, the line will be different.

Assumptions of Linear Regression

Now, that you know what constitutes a linear regression, we shall go into the assumptions of linear regression.

Here are the assumptions of linear regression.

1. The Two Variables Should be in a Linear Relationship

The first assumption of simple linear regression is that the two variables in question should have a linear relationship.

The example of Sarah plotting the number of hours a student put in and the amount of marks the student got is a classic example of a linear relationship.

Yes, one can say that putting in more hours of study does not necessarily guarantee higher marks, but the relationship is still a linear one. There will always be many points above or below the line of regression. These points that lie outside the line of regression are the outliers.

The assumption of linear regression extends to the fact that the regression is sensitive to outlier effects. This assumption is also one of the key assumptions of multiple linear regression.

2. All the Variables Should be Multivariate Normal

The first assumption of linear regression talks about being ina linear relationship. The second assumption of linear regression is that all the variables in the data set should be multivariate normal.

In other words, it suggests that the linear combination of the random variables should have a normal distribution. The same example discussed above holds good here, as well.

The students reported their activities like studying, sleeping, and engaging in social media. Now, all these activities have a relationship with each other. If you study for a more extended period, you sleep for less time. Similarly, extended hours of study affects the time you engage in social media.

Thus, this assumption of simple linear regression holds good in the example. It is possible to check the assumption using a histogram or a Q-Q plot.

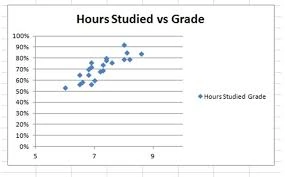
3. There Should be No Multicollinearity in the Data

Another critical assumption of multiple linear regression is that there should not be much multicollinearity in the data. Such a situation can arise when the independent variables are too highly correlated with each other.

In our example, the variable data has a relationship, but they do not have much collinearity. There could be students who would have secured higher marks in spite of engaging in social media for a longer duration than the others.

Similarly, there could be students with lesser scores in spite of sleeping for lesser time. The point is that there is a relationship but not a multicollinear one.

If you still find some amount of multicollinearity in the data, the best solution is to remove the variables that have a high variance inflation factor.

This assumption of linear regression is a critical one.

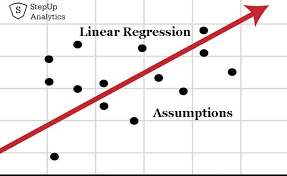
4. There Should be No Autocorrelation in the Data

One of the critical assumptions of multiple linear regression is that there should be no autocorrelation in the data. When the residuals are dependent on each other, there is autocorrelation. This factor is visible in the case of stock prices when the price of a stock is not independent of its previous one.

Plotting the variables on a graph like a scatterplot allows you to check for autocorrelations if any. Another way to verify the existence of autocorrelation is the Durbin-Watson test.

5. There Should be Homoscedasticity Among the Data

Finally, the fifth assumption of a classical linear regression model is that there should be homoscedasticity among the data. The scatterplot graph is again the ideal way to determine the homoscedasticity. The data is said to homoscedastic when the residuals are equal across the line of regression. In other words, the variance is equal.

The Breusch-PaganTest is the ideal one to determine homoscedasticity. The Goldfield-Quandt Test is useful for deciding heteroscedasticity.

We have seen the five significant assumptions of linear regression.

Examples of Assumptions of Simple Linear Regression in a Real-Life Situation

Here are some cases of assumptions of linear regression in situations that you experience in real life.

(i) Predicting the amount of harvest depending on the rainfall is a simple example of linear regression in our lives. There is a linear relationship between the independent variable (rain) and the dependent variable (crop yield).

(ii) The higher the rainfall, the better is the yield. At the same time, it is not a deterministic relation because excess rain can cause floods and annihilate the crops.

(iii) Another example of the assumptions of simple linear regression is the prediction of the sale of products in the future depending on the buying patterns or behavior in the past.

(iv) Economists use the linear regression concept to predict the economic growth of the country.

Making Predictions with Linear Regression

One of the advantages of the concept of assumptions of linear regression is that it helps you to make reasonable predictions. A simple example is the relationship between weight and height.

We have seen that weight and height do not have a deterministic relationship such as between Centigrade and Fahrenheit.

In the case of Centigrade and Fahrenheit, this formula is always correct for all values.
C/5 = (F – 32)/9

In the case of the weight and height relationship, there is no set formula, as such. However, the linear regression model representation for this relationship would be

Y = B0 + B1*x1 where y represents the weight, x1 is the height, B0 is the bias coefficient, and B1 is the coefficient of the height column.

The assumption of the classical linear regression model comes handy here.

Let us assume that B0 = 0.1 and B1 = 0.5. Using these values, it should become easy to calculate the ideal weight of a person who is 182 cm tall.

Weight = 0.1 + 0.5(182) entails that the weight is equal to 91.1 kg. Using this formula, you can predict the weight fairly accurately. However, there could be variations if you encounter a sample subject who is short but fat. This formula will not work. Hence, you need to make assumptions in the simple linear regression to predict with a fair degree of accuracy. The same logic works when you deal with assumptions in multiple linear regression.

Assumptions of Classical Linear Regression Model

As long as we have two variables, the assumptions of linear regression hold good. However, there will be more than two variables affecting the result. In our example itself, we have four variables,

• number of hours you study – X1
• number of hours you sleep – X2
• Number of hours you engage in social media – X3
• Your final marks – Y

Assumptions of Classical Linear Regression Model

In this case, the assumptions of the classical linear regression model will hold good if you consider all the variables together.

1. The Regression Model should be Linear in its Coefficients as well as the Error Term

This formula will hold good in our case
Y = B0 + B1X1 + B2X2 + B3X3 + € where € is the error term.

2. The Error Term should have a Population Mean of Zero

The error term is critical because it accounts for the variation in the dependent variable that the independent variables do not explain. Therefore, the average value of the error term should be as close to zero as possible for the model to be unbiased.

3. All the Independent Variables in the Equation are Uncorrelated with the Error Term

In case there is a correlation between the independent variable and the error term, it becomes easy to predict the error term. It violates the principle that the error term represents an unpredictable random error. Therefore, all the independent variables should not correlate with the error term.

4. Observations of the Error Term should also have No Relation with each other

The rule is such that one observation of the error term should not allow us to predict the next observation.

5. The Error Term should be Homoscedastic (it should have a constant variance)

This assumption of the classical linear regression model entails that the variation of the error term should be consistent for all observations. Plotting the residuals versus fitted value graph enables us to check out this assumption.

6. None of the Independent Variables should be a Linear Function of the other Variables

When the two variables move in a fixed proportion, it is referred to as a perfect correlation. For example, any change in the Centigrade value of the temperature will bring about a corresponding change in the Fahrenheit value. This assumption of the classical linear regression model states that independent values should not have a direct relationship amongst themselves.

Final Thoughts

We have seen the concept of linear regressions and the assumptions of linear regression one has to make to determine the value of the dependent variable. Making assumptions of linear regression is necessary for statistics. If these assumptions hold right, you get the best possible estimates. In statistics, the estimators producing the most unbiased estimates having the smallest of variances are termed as efficient.

The classical linear regression model is one of the most efficient estimators when all the assumptions hold. The best aspect of this concept is that the efficiency increases as the sample size increases to infinity. To understand the concept in a more practical way, you should take a look at the linear regression interview questions.

Finally, we can end the discussion with a simple definition of statistics.
“Statistics is that branch of science where two sets of accomplished scientists sit together and analyze the same set of data, but still come to opposite conclusions.”

If you want to build a career in Data Analytics, take up the Data Analytics using Excel Course today.